Linear programming method is a type of constrained optimization method of project selection. In this method, you look towards reducing the project cost by efficiently reducing the duration of the project. You look for running an activity in its normal time or the crash time. The crash time of the activity enables you to reduce the activity time or the project as a whole.
When you complete only a specific activity for a duration that incurs the smallest cost, you term it as the normal time. You crash an activity by spending more efforts to make sure that the activity takes lesser time to complete. Adding efforts to the activity definitely increases the cost. However, when you include overhead costs, you might realize that running multiple activities at crash level is financially advantageous, if it reduces the overall duration and overhead costs.
However, one of the most important aspects of the project you need to consider is if crashing an activity reduces the overall time of the project. For example, if the activity does not lie in the critical path of the project, then you might not want to consider crashing the activity. Critical path of the project is the sequence of the activities that you need to perform from start to end, considering that you can perform other activities, which can be another sequence of activities, in parallel. The alternate sequence of activities that you perform in parallel is known as an alternate path.
At times, you might realize that crashing activities in the critical path might result in making an alternate path a critical path because the time required to complete such path is now more than the former critical path. In such a case, if you justify the costs involved, you can consider further crashing the activities of the new critical path too.
Crashing an activity means that you reduce the time required to complete the activity by adding additional resources, including man power and machinery. This not only adds efforts and reduces the time required to complete the activity faster, but also increases the cost for completing the activity.
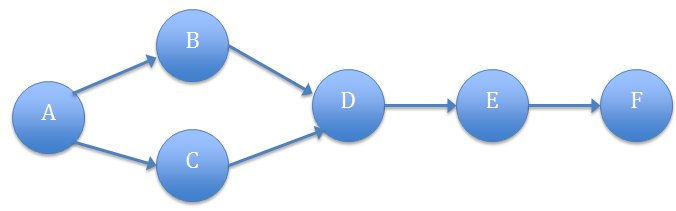
Consider the following table of activities for a simple project that indicates the normal and crash time along with the costs of various activities of a project. The table also indicates the dependencies of various activities:
| Activity | Predecessor | Normal | Crash | ||
|---|---|---|---|---|---|
| Week | Cost | Week | Cost | ||
| A | – | 2 | 80 | 1 | 150 |
| B | A | 3 | 90 | 2 | 120 |
| C | A | 4 | 120 | 2 | 180 |
| D | B, C | 2 | 100 | 2 | 100 |
| E | D | 1 | 50 | 1 | 50 |
| F | E | 1.5 | 200 | 0.5 | 300 |
Consider the activity F. This activity requires four weeks to complete. However, you can crash this activity to two weeks with an additional cost of $ 150. However, there is always proportionality between the time of reduction and additional cost. Therefore, if you want to crash the activity F by two weeks, you can calculate the cost of activity by calculating the slope cost and then the cost of activity as follows:
Slope Cost = (Crash Cost – Normal Cost) / (Normal time - Crash time)
Cost of Activity = Normal Cost + (Slope Cost * Crash time)
Applying the preceding formulas, we can calculate the activity cost of activity F as:
Slope Cost = (300 – 200) / 1
= 100
Cost of activity = 200 + (100 * 0.5)
= 250
You can calculate the cost of activity for each activity and sum all of the costs to arrive at the final cost of project. You can also represent the activities from the table with a network diagram to understand the dependencies of the activities. The following is the network diagram for the sample project: