Dynamic programming method is yet another constrained optimization method of project selection. In this method, you break a complex problem into a sequence of simpler problems. This method provides a general framework of analyzing many problem types. In this framework, you use various optimization techniques to solve a specific aspect of the problem. This method requires your creativity before you can decide if the problem needs to use dynamic programming for its solution.
This method of project selection is a mathematical technique to make a sequence of correlated decisions. The method consists of systematic procedure to determine the best combination of decisions. In the linear programming method of project selection, you have standard mathematical formula. However, in case of the dynamic programming method of project selection, you do not have any standard mathematical formula.
In the dynamic programming method, you use a general method to solve a problem. You must develop the equations used to solve the problem to the requirement of the problem.
Features of Dynamic Programming Method
The dynamic programming method of projects selection has the following features:
Stages
In the dynamic programming method, you structure the problem in multiple stages. You solve each of these stages sequentially, one at a time. Even though you solve one stage at a time, the solution of the problem in one stage defines the characteristics of the problem in the next stage. On a time line of the project planning, you represent each stage at different time frames. However, at times you might realize that some stages do not have any time association. When you formulate a dynamic program for a problem that has such stages, it becomes difficult to recognize the problems.
States
When you define a stage for a problem, you also associate it with a state of the process. The state of a process is the information you need to assess the effect of the decision has on the future action. You do not have to follow any set rules to specify a state. However, it is a critical parameter for dynamic programming method. Specifying a state is more of an art, and requires creativity and deep understanding of the problem.
You must consider the following properties of a state when specifying it:
- You should keep the number of state variables to the minimal because of the cost involved in the computation efforts.
- You must provide sufficient information to enable future decision without considering process used to reach the state.
Recursive Optimization
After you have structured stages and states associated to the stages, you need to develop a recursive optimization procedure. The recursive optimization procedure builds a solution of up to the n number of stages, with one stage at a time in the specified sequence. The recursive procedure solves each stage until an overall optimum solution is available.
You can base the recursive procedure on any of the following induction processes:
- Forward induction process: The recursive procedure starts with the first stage and concludes with the last stage by including each stage sequentially, one stage at a time.
- Backward induction process: The recursive procedure starts with the last stage and concludes with the first stage by including each stage sequentially, one stage at a time, in the reverse order.
Mathematical Formula
Consider that you have a multistage decision process where the return of the specific stage is represented by the following function (f):
![]()
Here:
- dn: is the decision that you can chose form the set Dn.
- sn: is the state of the process with n stages remaining in the N number of stages in the procedure.
The next state of the process completely depends on the current state and decision of the process. Therefore, you can define the transition function (t) with n-1 stages to be remaining in the procedure as:
![]()
Now that the dynamic programming method consists of a recursive optimization procedure, you can use the following optimal value function, which represents the maximum return possible over the n stages remaining:
Subject to:
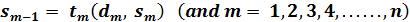
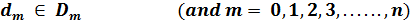
The function uses only the decision variable and not the decision variable . Therefore, you can first maximize the latter part of the equation and then chose to maximize the entire equation.
You can now rewrite the equation as follows:

